Пересечение 3D-лучей (ближайшая точка).
Хотите разобраться в математической теории, лежащей в основе 3D-лучей? Предлагаем простое руководство по применению таких математических инструментов, как псевдообратные матрицы, оптимизация с помощью наименьших квадратов, метод Крамера, смешанное произведение. Введение Актуальность темы
В таких областях, как компьютерная графика, навигация для беспилотников и дополненная реальность, где за счет 3D-моделирования создаются захва?
Пересечение 3D-лучей (ближайшая точка)...
Хотите разобраться в математической теории, лежащей в основе 3D-лучей? Предлагаем простое руководство по применению таких математических инструментов, как псевдообратные матрицы, оптимизация с помощью наименьших квадратов, метод Крамера, смешанное произведение.
Введение
Актуальность темы
В таких областях, как компьютерная графика, навигация для беспилотников и дополненная реальность, где за счет 3D-моделирования создаются захватывающие впечатления, знание алгоритмов пересечения лучей и триангуляции позволяет дата-сайентистам создавать правдоподобные имитации и интерактивные виртуальные миры.
Подобные практики доказывают, что математические концепты, такие как псевдообратные матрицы, оптимизация с помощью наименьших квадратов, метод Крамера, смешанное произведение, — не просто сухая теория. Это практические инструменты, помогающие решать реальные задачи.
Определение луча
Луч — это прямая, которая начинается из конкретной точки и тянется бесконечно долго в определенном направлении, как лазерный луч или луч света.
Считайте, что луч — это улица с односторонним движением и фиксированной начальной точкой, а линия — это улица с двусторонним движением, которая тянется бесконечно в обоих направлениях.
С математической точки зрения луч определяется началом координат o и направлением d. Поскольку это одномерное пространство, любая точка вдоль луча параметризуется положительным расстоянием (или временем) t по отношению к началу координат.
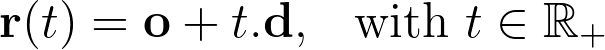
Пересечение лучей
Найти пересечение двух лучей r1 и r2 — значит найти два параметра t1 и t2 соответственно на первом и втором лучах, что приводит к нахождению одной и той же точки в пространстве.
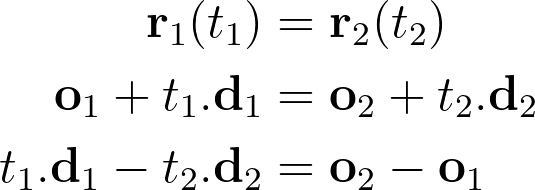
Стоит отметить, что размерность пространства, в котором находится луч, не указана. Он может быть двухмерным, как линия, нарисованная на листе бумаги, трехмерным, как лазерный луч, или даже существовать в более высоких размерностях.
Поскольку необходимо найти значения t1 и t2, объединим их в вектор-столбец x. Это позволит векторизовать уравнение в каноническую линейную систему Ax=b. Для большей наглядности под каждым членом помещена аннотация, указывающая форму матрицы или вектора, а n — размерность пространства, в котором определяется луч.
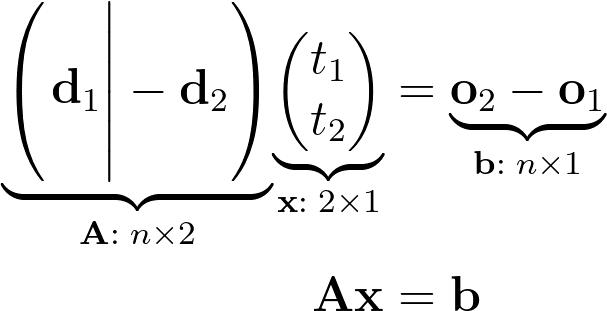
Важно: матрица A строится путем одновременной конкатенации двух направлений в виде векторов-столбцов, причем второй из них инвертирован.
Решение Ax=b дает t1 и t2. Но если один из этих параметров отрицателен, точка пересечения будет находиться за одним из начал лучей, то есть оба луча не пересекаются.
2. Пересечение 2D-лучей
Введение
Случай 2D — самый простой. Как правило, две 2D-прямые, если только они не абсолютно параллельны, всегда сходятся в единственной общей точке.
На изображении ниже r1 и r2 пересекаются. Однако r3 не пересекает ни один луч, потому что он параллелен r2 и встречается с r1 за его началом.
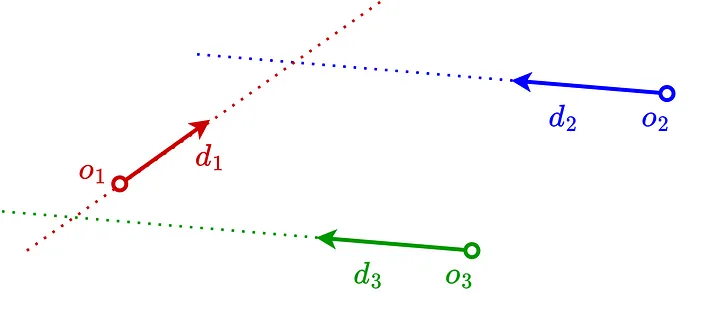
Решение линейной системы
Система линейных уравнений Ax=b, представленная выше, имеет n уравнений и 2 неизвестных. Таким образом, в двумерном случае получаем систему из 2 уравнений и 2 неизвестных. Это означает, что нужно просто инвертировать матрицу A.
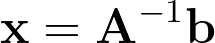
Если лучи параллельны, матрица A не будет инвертируемой, поскольку два ее столбца, d1 и -d2, будут коллинеарны.
Если нас не интересуют t1 и t2 и нужно просто узнать, есть ли пересечение, достаточно вычислить определитель A и сравнить его с 0.
Если нам не нужны как t1, так и t2, например если необходимо найти фактическое двумерное положение точки пересечения, разумно будет использовать метода Крамера. Он предлагает решение с помощью определителей A и модифицированных матриц, где один столбец A заменен на b.
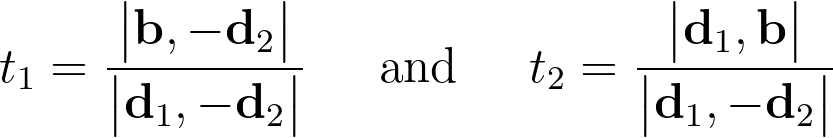
Пересечение 3D-лучей
Введение
В отличие от случая 2D, пересечение двух 3D-лучей крайне маловероятно. Например, попытка заставить пересечься лучи от двух лазерных указок, которые держат два человека, очень сложна.
Линейная система Ax=b в итоге состоит из 3 уравнений для 2 неизвестных, что делает ее неразрешимой, если только в уравнениях нет избыточности.
Метод наименьших квадратов
Учитывая отсутствие решения в большинстве случаев, кратчайший отрезок прямой между двумя лучами можно рассматривать как их пересечение. Обозначим p1 и p2 как конечные точки этого оптимального отрезка, расположенные на r1 и r2 соответственно.
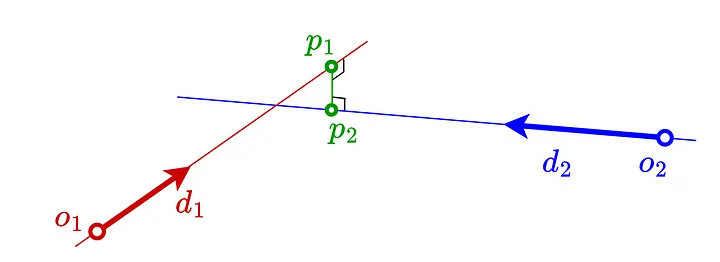
Теперь наша задача превращается в минимизацию по методу наименьших квадратов. Ее формулировка проста, учитывая, что Ax-b уже представляет собой вектор между p2 и p1.
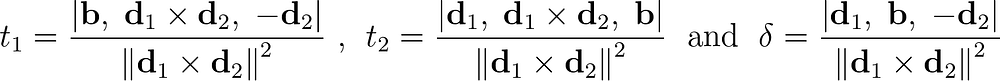
Это хорошо известная задача. Обнуление градиента в оптимальной точке позволяет применить решение с помощью псевдообратной матрицы. Таким образом находим удобный способ построения квадратной и, следовательно, инвертируемой матрицы.

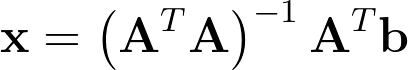
Ортогональность
На графике выше видно, что кратчайший отрезок перпендикулярен обоим лучам, но нам еще предстоит формально доказать это, хотя такое утверждение кажется верным на уровне интуиции.
Нулевой градиент также подразумевает, что скалярное произведение между отрезком, определяемым p1 и p2, и обоими направлениями лучей d1 и d2 равно нулю, что доказывает ортогональность.
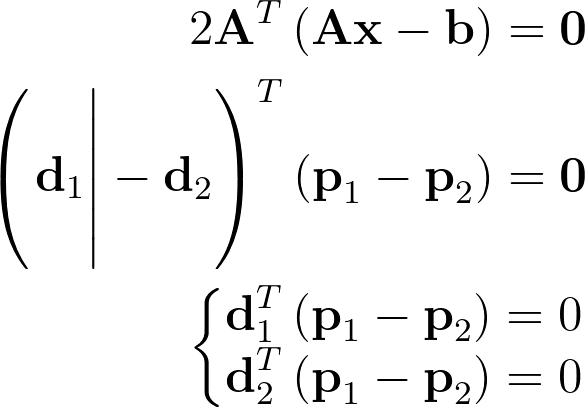
Альтернативная линейная система
Метод наименьших квадратов работает отлично, но мы можем ввести третью неизвестную переменную, чтобы сделать эту линейную систему разрешимой.
Учитывая, что векторы d1, d2 и p2-p1 представляют собой ортогональный базис, можно построить ортогональную рамку с o1 в качестве начала координат. Тогда получаем точки p1 и p2 , выразив локальные координаты o2 относительно этой рамки.
Знаковую длину отрезка p2-p1 обозначим как δ. Заметим, что направление отрезка задается перекрестным произведением обоих направлений лучей.
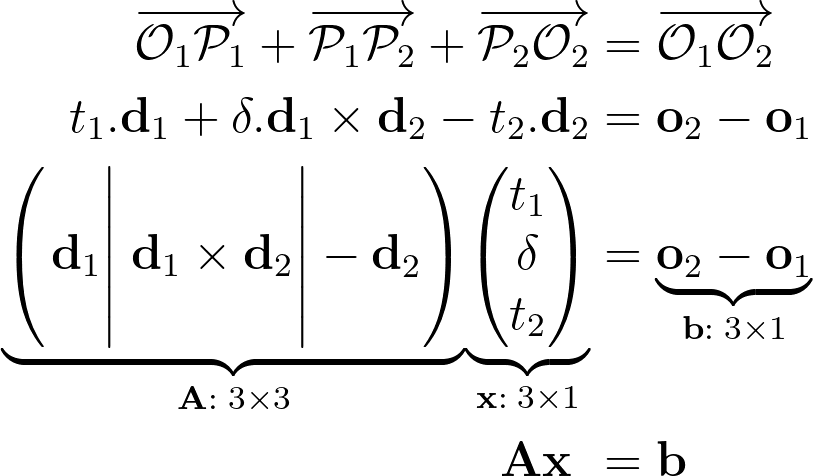
Определитель матрицы 3×3 можно получить с помощью смешанного произведения, которое включает в себя скалярное произведение одного столбца на перекрестное произведение двух других.
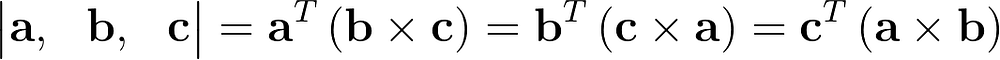
В данном случае упрощение уравнения с определителем не вызывает затруднений, поскольку второй столбец уже представляет собой перекрестное произведение. Заметим, что вставка перекрестного произведения в качестве последнего столбца привела бы к отрицанию нормы.
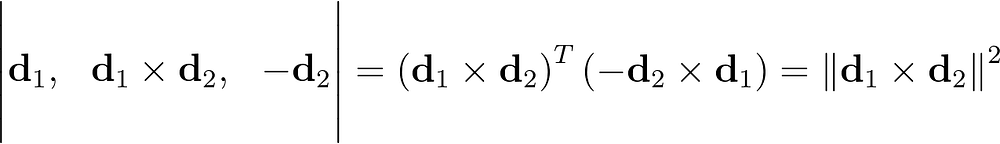
Решение с помощью метода Крамера дает оптимальные t1 и t2, а также знаковую длину δ кратчайшего отрезка.
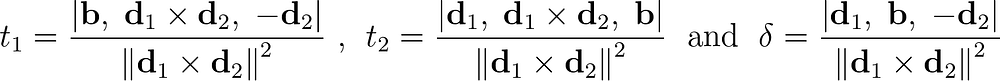
Любители чистых уравнений могут изменить порядок и поменять местами столбцы, чтобы убрать минусы и оптимизировать внешний вид.
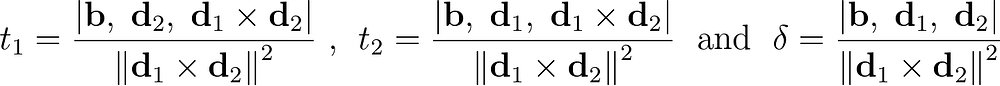
Точка пересечения
Точку пересечения можно определить как середину кратчайшего отрезка, то есть 0.5(p1+p2).
