Визуализация параметров градиентного спуска в Torch.
Простые интерфейсы современных фреймворков машинного обучения (МО) таят в себе множество сложностей. С таким количеством регуляторов и переключателей можно легко впасть в карго-культ программирования, если не понимать, что происходит за всем этим. Рассмотрим несколько важных параметров оптимизатора стохастического градиентного спуска (SGD) в Torch: def torch.optim.SGD(
params, lr=0.001, momentum=0, dampening=0,
weight_decay=0, nesterov=False, *, maximize=False,
foreach=None, differentiable=False)
Визуализация параметров градиентного спуска в Torch...
Простые интерфейсы современных фреймворков машинного обучения (МО) таят в себе множество сложностей. С таким количеством регуляторов и переключателей можно легко впасть в карго-культ программирования, если не понимать, что происходит за всем этим. Рассмотрим несколько важных параметров оптимизатора стохастического градиентного спуска (SGD) в Torch:
def torch.optim.SGD(
params, lr=0.001, momentum=0, dampening=0,
weight_decay=0, nesterov=False, *, maximize=False,
foreach=None, differentiable=False):
# Реализует стохастический градиентный спуск (опционально с импульсом).
# ...Помимо привычных коэффициентов скорости обучения (lr) и импульса (momentum), есть еще несколько параметров, которые оказывают значительное влияние на обучение нейронных сетей. В этой статье будет наглядно показано влияние этих параметров на выполнение простой задачи МО с различными функциями потерь.
Демонстрационная задача
Для начала выполним демонстрационную задачу: построим линейную регрессию по набору точек. Чтобы сделать ее более интересной, применим квадратичную функцию плюс шум, так что нейронной сети придется искать компромиссные решения, а мы сможем увидеть большее влияние функций потерь:
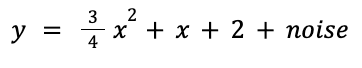
Пока просто используем numpy и matplotlib для визуализации данных — torch пока не требуется:
import numpy as np import matplotlib.pyplot as plt np.random.seed(20240215) n = 50 x = np.array(np.random.randn(n), dtype=np.float32) y = np.array( 0.75 * x**2 + 1.0 * x + 2.0 + 0.3 * np.random.randn(n), dtype=np.float32) plt.scatter(x, y, facecolors='none', edgecolors='b') plt.scatter(x, y, c='r') plt.show()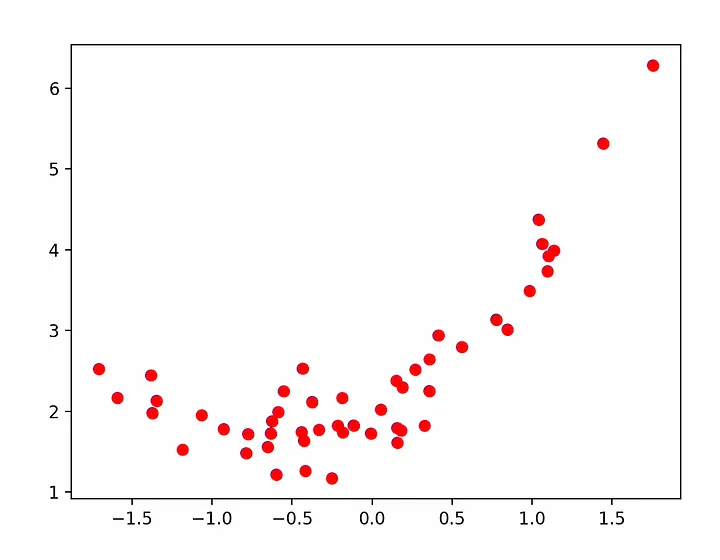
Теперь развернем torch и представим простой цикл обучения для сети с одним нейроном. Чтобы получить устойчивые результаты при изменении функции потерь, будем каждый раз начинать обучение с одного и того же набора параметров. При этом первым “предположением” нейрона будет уравнение y = 6*x — 3 (на которое будем воздействовать через параметры weight и bias нейрона):
import torch model = torch.nn.Linear(1, 1) model.weight.data.fill_(6.0) model.bias.data.fill_(-3.0) loss_fn = torch.nn.MSELoss() learning_rate = 0.1 epochs = 100 optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate) for epoch in range(epochs): inputs = torch.from_numpy(x).requires_grad_().reshape(-1, 1) labels = torch.from_numpy(y).reshape(-1, 1) optimizer.zero_grad() outputs = model(inputs) loss = loss_fn(outputs, labels) loss.backward() optimizer.step() print('epoch {}, loss {}'.format(epoch, loss.item()))Запустив это, получаем текстовый вывод, который показывает, что потери уменьшаются и в конечном итоге снижаются до минимума, как и ожидалось:
epoch 0, loss 53.078269958496094
epoch 1, loss 34.7295036315918
epoch 2, loss 22.891206741333008
epoch 3, loss 15.226042747497559
epoch 4, loss 10.242652893066406
epoch 5, loss 6.987757682800293
epoch 6, loss 4.85075569152832
epoch 7, loss 3.4395809173583984
epoch 8, loss 2.501774787902832
epoch 9, loss 1.8742430210113525
...
epoch 97, loss 0.4994412660598755
epoch 98, loss 0.4994412362575531
epoch 99, loss 0.4994412660598755Для визуализации подгонки извлечем из нейрона усвоенные параметры смещения (bias) и веса (weight) и построим график подгонки по точкам:
weight = model.weight.item()
bias = model.bias.item()
plt.scatter(x, y, facecolors='none', edgecolors='b')
plt.plot(
[x.min(), x.max()],
[weight * x.min() + bias, weight * x.max() + bias],
c='r')
plt.show()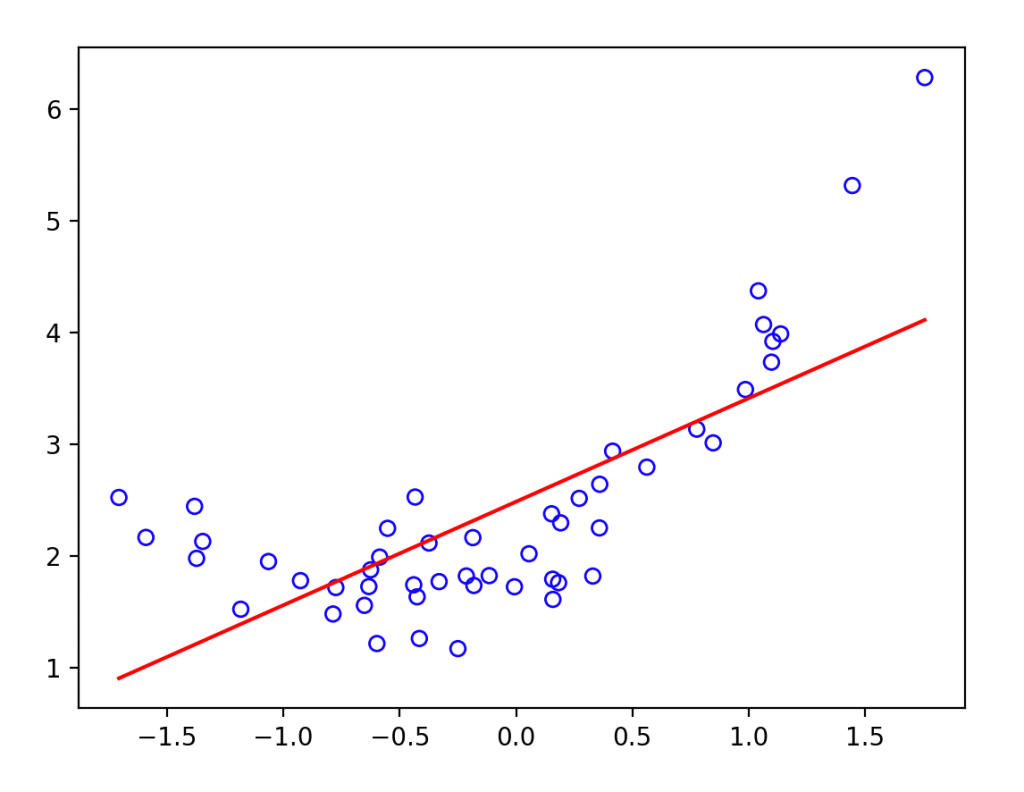
Визуализация функции потерь
Вышеописанное кажется разумным, но до сих пор все решалось с помощью высокоуровневых функций Torch, таких как optimizer.zero_grad(), loss.backward() и optimizer.step(). Чтобы понять, куда двигаться дальше, нужно визуализировать путь, который проходит модель через функцию потерь. Для визуализации потерь сделаем выборку в сетке размером 101 на 101 точку, а затем построим график с помощью imshow:
def get_loss_map(loss_fn, x, y): """Maps the loss function on a 100-by-100 grid between (-5, -5) and (8, 8).""" losses = [[0.0] * 101 for _ in range(101)] x = torch.from_numpy(x) y = torch.from_numpy(y) for wi in range(101): for wb in range(101): w = -5.0 + 13.0 * wi / 100.0 b = -5.0 + 13.0 * wb / 100.0 ywb = x * w + b losses[wi][wb] = loss_fn(ywb, y).item() return list(reversed(losses)) # Поскольку ось y будет инвертирована import pylab loss_fn = torch.nn.MSELoss() losses = get_loss_map(loss_fn, x, y) cm = pylab.get_cmap('terrain') fig, ax = plt.subplots() plt.xlabel('Bias') plt.ylabel('Weight') i = ax.imshow(losses, cmap=cm, interpolation='nearest', extent=[-5, 8, -5, 8]) fig.colorbar(i) plt.show()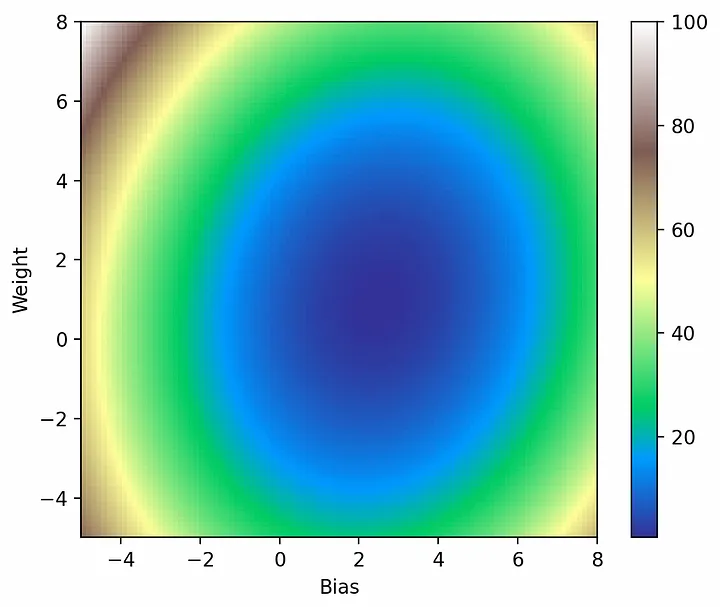
Теперь можно фиксировать параметры модели во время выполнения градиентного спуска, чтобы увидеть, как работает оптимизатор:
model = torch.nn.Linear(1, 1) ... models = [[model.weight.item(), model.bias.item()]] for epoch in range(epochs): ... print('epoch {}, loss {}'.format(epoch, loss.item())) models.append([model.weight.item(), model.bias.item()]) # Нанесение параметров модели на карту потерь. cm = pylab.get_cmap('terrain') fig, ax = plt.subplots() plt.xlabel('Bias') plt.ylabel('Weight') i = ax.imshow(losses, cmap=cm, interpolation='nearest', extent=[-5, 8, -5, 8]) model_weights, model_biases = zip(*models) ax.scatter(model_biases, model_weights, c='r', marker='+') ax.plot(model_biases, model_weights, c='r') fig.colorbar(i) plt.show()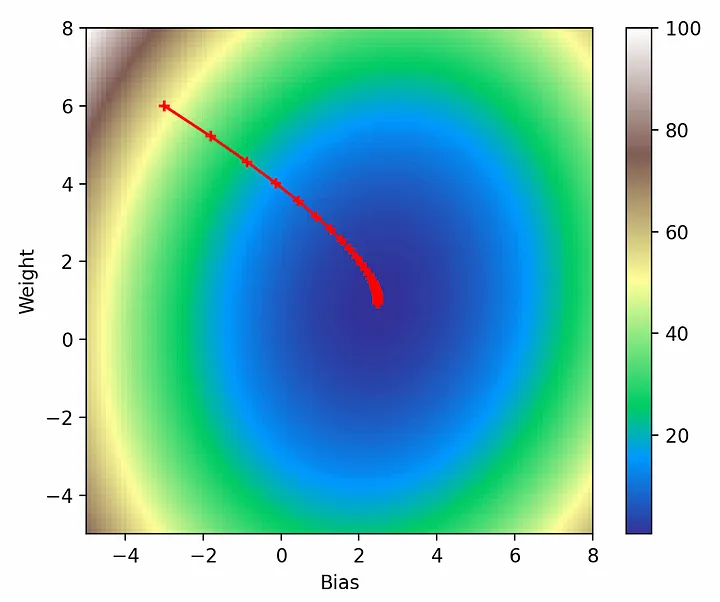
Все выглядит именно так, как и должно быть: модель начинает с инициализированных нами параметров (-3, 6), делает все более мелкие шаги в направлении градиента и в конце концов достигает глобального минимума.
Визуализация других параметров
Функция потерь
Теперь посмотрим, как другие параметры влияют на градиентный спуск. Прежде всего, это функция потерь, для которой использовалась стандартная L2-потеря:
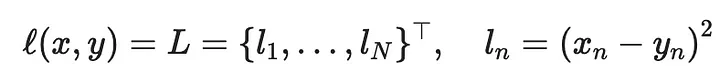
Но есть и другие функции потерь, которые можно было бы использовать:
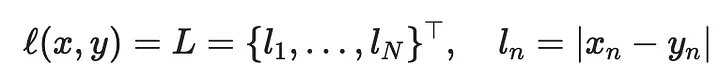
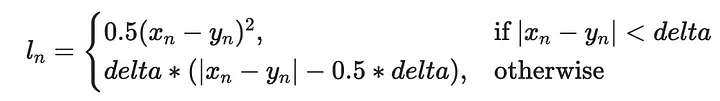
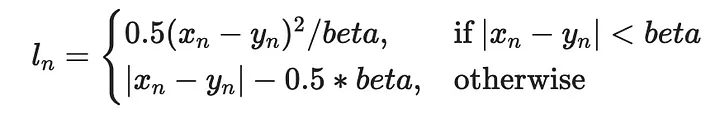
Обернем все, что сделали до сих пор, в цикл, чтобы опробовать все функции потерь и построить их вместе:
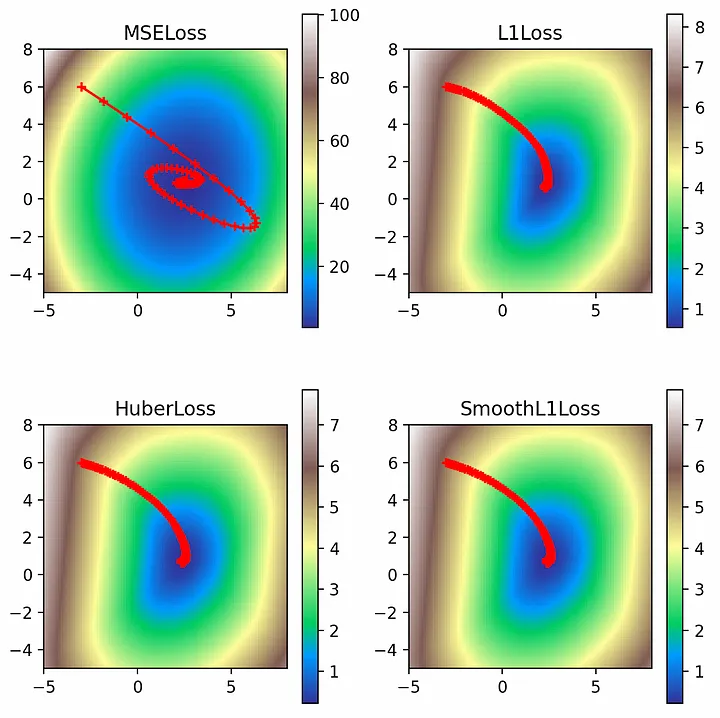
def multi_plot(lr=0.1, epochs=100, momentum=0, weight_decay=0, dampening=0, nesterov=False): fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2) for loss_fn, title, ax in [ (torch.nn.MSELoss(), 'MSELoss', ax1), (torch.nn.L1Loss(), 'L1Loss', ax2), (torch.nn.HuberLoss(), 'HuberLoss', ax3), (torch.nn.SmoothL1Loss(), 'SmoothL1Loss', ax4), ]: losses = get_loss_map(loss_fn, x, y) model, models = learn( loss_fn, x, y, lr=lr, epochs=epochs, momentum=momentum, weight_decay=weight_decay, dampening=dampening, nesterov=nesterov) cm = pylab.get_cmap('terrain') i = ax.imshow(losses, cmap=cm, interpolation='nearest', extent=[-5, 8, -5, 8]) ax.title.set_text(title) loss_w, loss_b = zip(*models) ax.scatter(loss_b, loss_w, c='r', marker='+') ax.plot(loss_b, loss_w, c='r') plt.show() multi_plot(lr=0.1, epochs=100)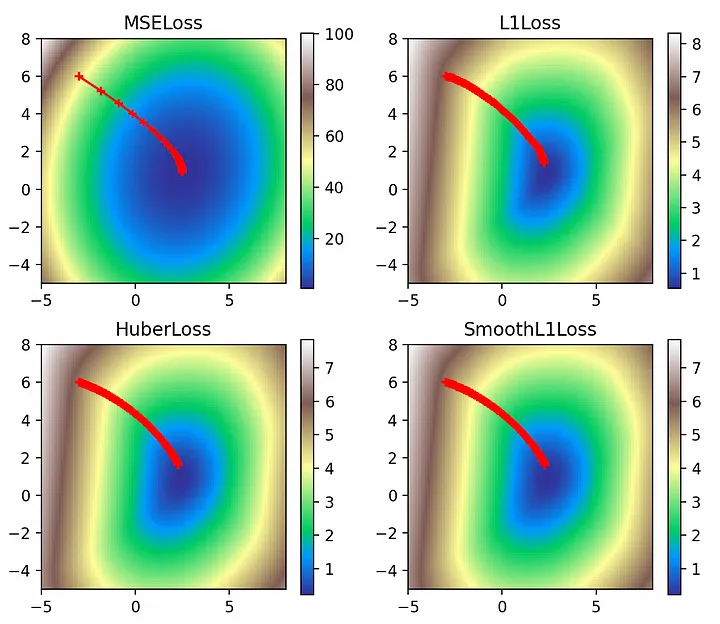
Здесь видим интересные контуры функций потерь, не относящихся к L2. Если функция потерь L2 является сглаженной и имеет большие значения вплоть до 100, то другие функции потерь имеют гораздо меньшие значения, поскольку отражают только абсолютные ошибки. Однако более крутой градиент L2-потерь означает, что оптимизатор быстрее приближается к глобальному минимуму, о чем свидетельствует большее расстояние между его ранними точками. В то же время L1-потери демонстрируют гораздо более плавное приближение к минимумам.
Импульс
Следующим интересным параметром является импульс (momentum), который определяет, сколько градиента последнего шага нужно добавить к текущему обновлению градиента при движении вперед. Обычно достаточно очень малых значений импульса, но для наглядности установим безумное значение 0,9 (не пытайтесь повторить это самостоятельно):multi_plot(lr=0.1, epochs=100, momentum=0.9)
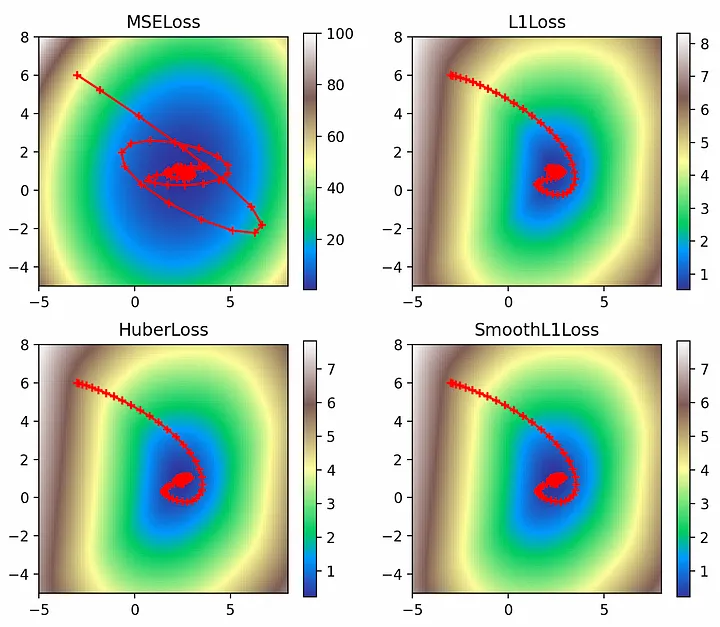
Благодаря запредельному значению импульса, можно наглядно представить его влияние на оптимизатор: он проскакивает глобальный минимум и вынужден кое-как возвращаться обратно. Наиболее ярко этот эффект проявляется в L2-потерях, крутые градиенты которых выносят его за пределы минимума и приближают к расхождению.
Импульс Нестерова
Импульс Нестерова — это интересная модификация обычного импульса. Обычный импульс добавляет часть градиента с последнего шага к градиенту для текущего шага, что приводит к сценарию, представленному на рисунке 7(a). Но если обычный импульс позволяет понять, куда выведет градиент с последнего шага, то импульс Нестерова вычисляет текущий градиент, предвидя, где это будет, что дает сценарий, представленный на рисунке 7(b):
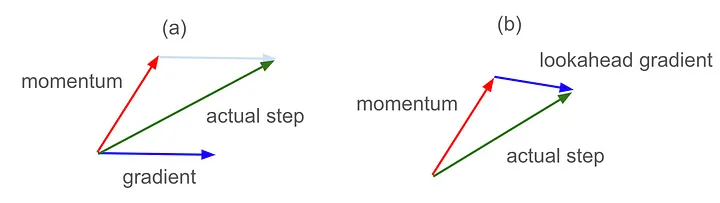
multi_plot(lr=0.1, epochs=100, momentum=0.9, nesterov=True)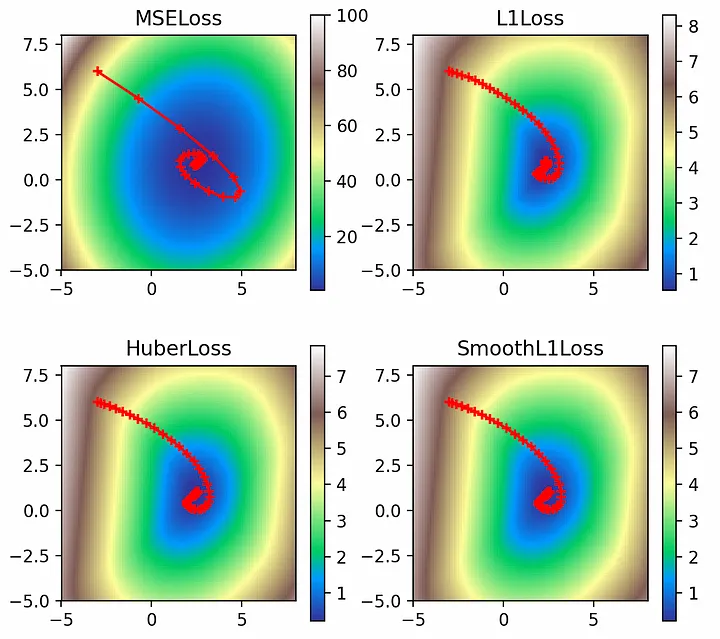
Судя по графическому представлению, импульс Нестерова сократил перехлест, который наблюдался при использовании обычного импульса. Особенно это заметно в случае L2: поскольку импульс пронес нас как раз над глобальным минимумом, использование импульса Нестерова для поиска места “приземления” позволило ввести компенсирующие градиенты с противоположной стороны целевой функции и фактически заранее скорректировать курс.
Сокращение весов
Сокращение весов позволяет ввести регулирующий L2-штраф для значения параметров (веса и смещения линейной сети):multi_plot(lr=0.1, epochs=100, momentum=0.9, nesterov=True, weight_decay=2.0)
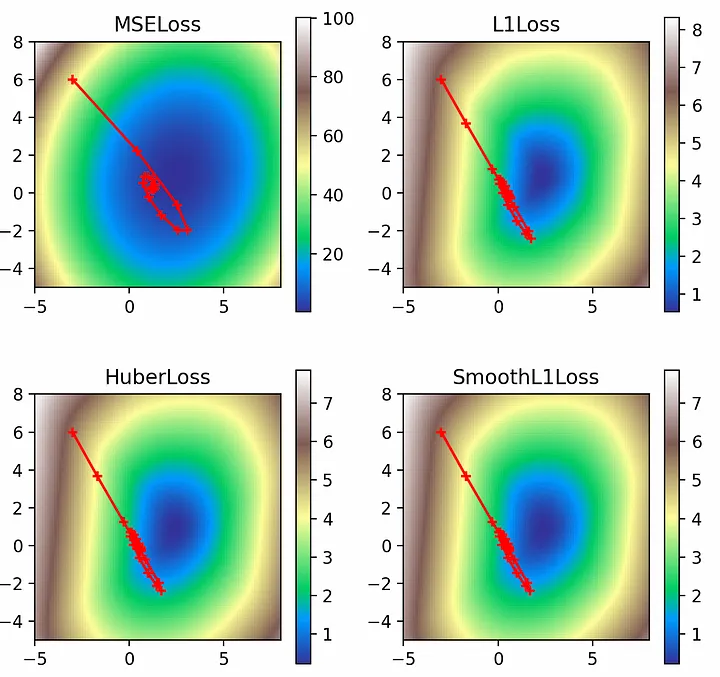
Во всех случаях регулирующий фактор уводит решения от их законных глобальных минимумов и приближает к началу координат (0, 0). Однако эффект наименее выражен в случае потерь L2, поскольку значения потерь достаточно велики, чтобы компенсировать штрафы L2 на весах.
Демпфирование
Наконец, следует рассмотреть демпфирование, которое уменьшает импульс на коэффициент демпфирования (dampening factor). Использование коэффициента демпфирования 0,8 позволяет эффективно сглаживать путь импульса через функцию потерь.multi_plot(lr=0.1, epochs=100, momentum=0.9, dampening=0.8)